Lista de símbolos básicos de matemáticas

Las matemáticas son un lenguaje universal que se utiliza en todo el mundo. Para los estudiantes del idioma inglés, comprender los símbolos matemáticos básicos puede ser clave para desbloquear este poderoso tema. En este artículo, exploramos varios símbolos comunes y sus significados, ayudándote a sentirte más seguro en tus estudios matemáticos.

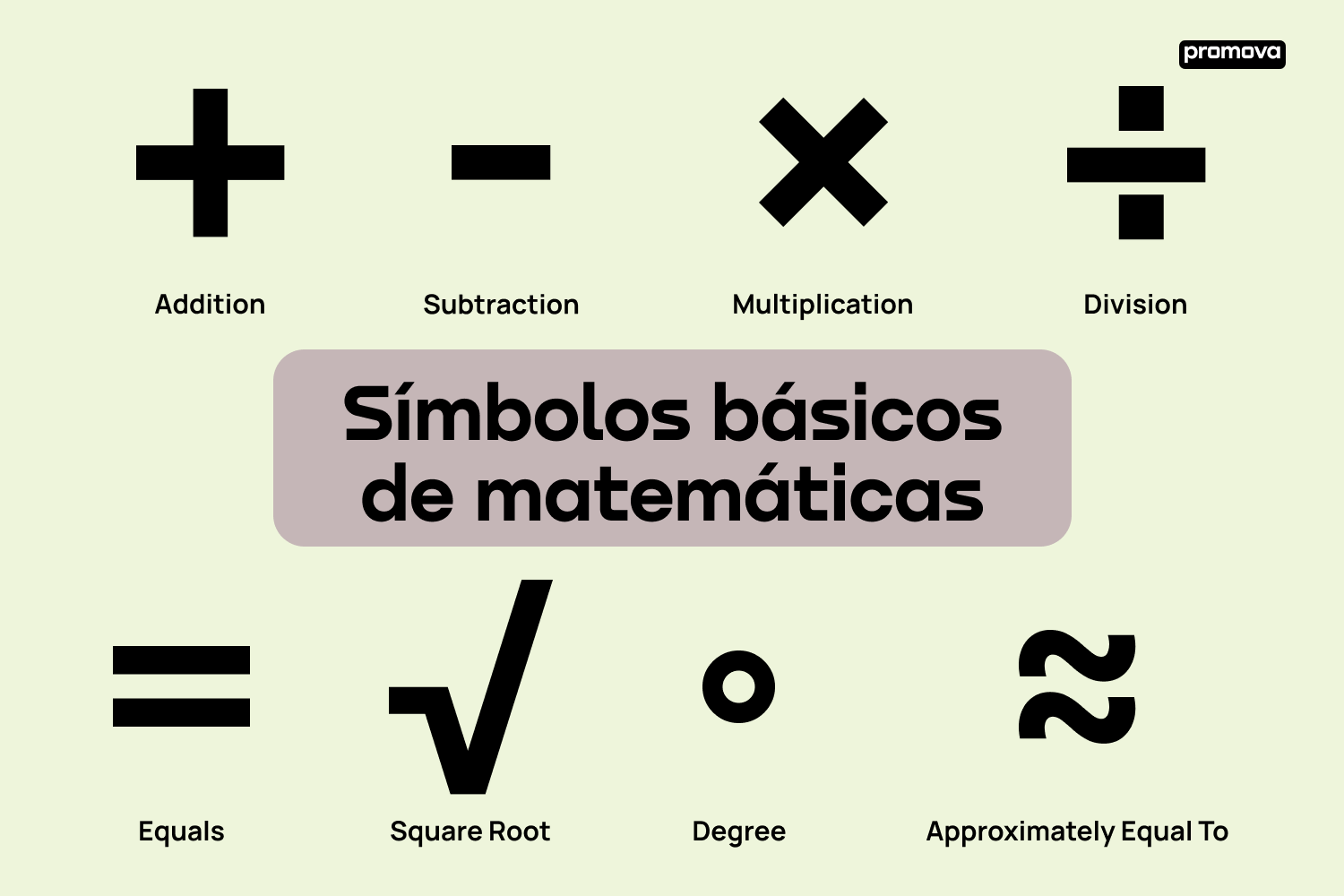
Símbolos de aritmética básica

Para aquellos que aprenden el idioma inglés, entender los símbolos matemáticos utilizados en la aritmética básica puede hacer que la comunicación matemática sea más accesible. Estos símbolos son fundamentales y aparecen en problemas matemáticos cotidianos.

• Addition (+) o Plus: se utiliza para sumar dos números; por ejemplo, 5 + 3 = 8.
• Subtraction (−) o Minus: se utiliza para restar un número de otro; por ejemplo, 9 − 6 = 3.
• Multiplication (×) o Times: se utiliza para multiplicar números; como em 4 × 2 = 8.
• Division (÷) o Divided by: se utiliza para dividir un número por otro; por ejemplo, 12 ÷ 4 = 3.

Familiarizándose con estos símbolos aritméticos básicos, has dado un paso importante en la comprensión de expresiones matemáticas en inglés. Este conocimiento te ayudará en varias tareas diarias y estudios.

Símbolos en álgebra

El álgebra a menudo contiene símbolos matemáticos que pueden tener nombres en inglés confusos. Estos símbolos en matemáticas son esenciales para formar y resolver ecuaciones, representar incógnitas y expresar relaciones.

• x, y, z: a menudo se utilizan para representar números desconocidos o variables; en la ecuación y = 2x + 3, x y y son variables.
• Equals (=): significa que dos expresiones son iguales; 5 = 5.
• Not equal (≠): muestra que dos expresiones no son iguales; 5 ≠ 6.
• Greater than (>): indica que un número es mayor que otro; 7 > 3.
• Less than (<): significa que un número es menor que otro; 2 < 5.
• Greater than or equal to (≥): muestra que un número es mayor o igual a otro; x ≥ 4.
• Less than or equal to (≤): indica que un número es menor o igual a otro; x ≤ 3.
• Ratio (:): una comparación de dos cantidades; la proporción de 4 a 8 es 1:2.
• Percent (%): una parte en cien; 50% significa la mitad.

Entender los símbolos matemáticos del álgebra y sus significados te ayudará a comprender expresiones matemáticas más complejas. Esta perspicacia te permitirá involucrarte con conceptos algebraicos en tus estudios futuros o en la vida cotidiana.

9

Símbolos en geometría

La geometría, con sus formas y relaciones únicas, tiene su propio conjunto de símbolos que pueden ser confusos. Estos símbolos ayudan a describir formas, ángulos y relaciones espaciales. Es importante conocer sus significados en inglés para comunicarse sobre matemáticas con confianza:

• Degree (°): una unidad de medida para ángulos; por ejemplo, 90° es un ángulo recto.
• Perpendicular (⊥): dos líneas que se intersectan en un ángulo de 90°; por ejemplo, “AB⊥CD” significa que la línea AB es perpendicular a la línea CD.
• Parallel (∥): dos líneas que corren en la misma dirección y nunca se encuentran; por ejemplo, “AB∥CD” significa que la línea AB es paralela a la línea CD.

Dominar estos símbolos de geometría puede mejorar tu comprensión de las matemáticas espaciales y conceptos de diseño. Ya sea en clase o en el trabajo, encontrarás estos símbolos matemáticos valiosos en muchas aplicaciones prácticas.

Lista de símbolos matemáticos avanzados

Las matemáticas avanzadas introducen símbolos que pueden ser completamente nuevos para aquellos que aprenden diferentes símbolos matemáticos en inglés. Aquí hay una lista de símbolos matemáticos utilizados en áreas especializadas como cálculo, lógica y teoría de números complejos.

• Union (∪): representa la combinación de dos conjuntos; incluye todos los elementos únicos de ambos conjuntos.
• Intersection (∩): denota los elementos comunes entre dos conjuntos; incluye solo los elementos que se encuentran en ambos conjuntos.
• Element of (∈): se utiliza para expresar que un objeto es un elemento de un conjunto; 3 ∈ {1, 2, 3}.
• Squared (²): se utiliza para indicar un número elevado al cuadrado; 3² = 9.
• Cubed (³): se utiliza para indicar un número elevado al cubo; 2³ = 8.
• Square Root (√): representa el valor no negativo que, multiplicado por sí mismo, da el número original; √9 = 3.
• Sine (sin): una función trigonométrica que representa la relación entre el lado opuesto a un ángulo y la hipotenusa en un triángulo rectángulo (por ejemplo, y=sin(x))
• Cosine (cos): otra función trigonométrica que representa la relación entre el lado adyacente a un ángulo y la hipotenusa en un triángulo rectángulo. (por ejemplo, y=cos(x))
• Infinity (∞): un concepto utilizado para describir algo sin límites; a menudo utilizado en límites.
• Approximately equal to (≈): se utiliza para mostrar que dos números son casi, pero no exactamente, iguales; π ≈ 3.14.
• Function (f(x)): representa una regla que asigna a cada entrada exactamente una salida; f(x) = 2x + 3 es una función lineal.
• Derivative (d/dx): significa la tasa a la cual una función está cambiando; utilizado en cálculo para encontrar pendientes de tangentes.
• Integral (∫): representa la acumulación de cantidades; utilizado en cálculo para encontrar áreas bajo curvas.
• Implies (⇒): utilizado en lógica para denotar que una declaración implica otra; “p⇒q” significa "si p entonces q".
• Equivalent (≡): utilizado en lógica para significar que dos declaraciones son lógicamente equivalentes; p ≡ q significa p implica q, q implica p.
• Prime (ℙ): se utiliza para describir números que solo tienen dos divisores: 1 y sí mismo; 2, 3, 5 son ejemplos de números primos.
• Mean (x̄): el promedio de un conjunto de números; se encuentra sumando todos los números y dividiendo por el conteo. Por ejemplo, x̄(4;8)=6.
• Standard Deviation (σ): mide la cantidad de variación o dispersión en un conjunto de valores.
• Transpose (T): cambia las filas y columnas entre sí en una matriz; utilizado para reorientar datos en álgebra lineal.
• Dot Product (·): representa la suma de los productos de las entradas correspondientes de dos secuencias de números; utilizado en la multiplicación de vectores.
• Imaginary Unit (i): la raíz cuadrada de −1; utilizado en números complejos para definir números que no son reales.
• Congruent (≅): se utiliza para describir figuras que tienen el mismo tamaño y forma; dos triángulos son congruentes si sus lados y ángulos correspondientes son iguales.
• Pi (π): una constante matemática que representa la relación entre la circunferencia de un círculo y su diámetro; aproximadamente 3.14159.
• For all (∀): denota que una declaración se sostiene para todos los miembros de un cierto conjunto o grupo; utilizado en lógica y teoría de conjuntos.
• There exists (∃): se utiliza para especificar que hay al menos un elemento que satisface una propiedad particular; también utilizado en lógica y teoría de conjuntos.

Comprender estos nombres de símbolos matemáticos avanzados te permitirá adentrarte en estudios matemáticos de nivel superior. Para los estudiantes del idioma inglés que aspiran a especializarse en matemáticas o campos relacionados, este entendimiento será un activo significativo.

Conclusión

Comprender estos símbolos matemáticos básicos es esencial para cualquier persona que aprenda matemáticas, especialmente para aquellos que la estudian en un nuevo idioma. Familiarizándose con diferentes símbolos matemáticos, podrás interpretar mejor las expresiones y ecuaciones matemáticas y sentirte más cómodo en tus estudios. Ya seas un estudiante o un aprendiz de por vida, los símbolos matemáticos son la base para entender conceptos matemáticos, permitiéndote construir tu conocimiento y explorar ideas más complejas.